Machine Learning with Finance Data (Forex) in R, H2O and MinIO
Forex (Foreign exchange) offers a wealth of data and opportunities to apply machine learning.
In this tutorial, I will use R, H2O, and MinIO to build a very simple statistical arbitrage model using foreign exchange (Forex) data. I’m using TraderMade as the source for the forex data. You can read more about TraderMade’s forex feed in How to Import Forex Data in R. I began by signing up for a free account and getting an api_key. Free accounts have limitations but will work well for this tutorial.
If you are not familiar with H2O, it is an open-source distributed in-memory machine learning environment. I described H2O more fully in an earlier post, Machine Learning Using H20, R, and MinIO.
The R programming language for statistical computing is used by statisticians and data miners for data analysis. I described R more fully in an earlier post, MinIO and Apache Arrow Using R. R is rather intuitive for working with data, data analysis, and machine learning.
The R language has a companion IDE called RStudio, which I will use for this development.
MinIO is high-performance software-defined S3-compatible object storage, making it a powerful and flexible replacement for Amazon S3. MinIO works seamlessly with cloud-native analytics and ML/AI frameworks.
Please install R and RStudio, have access to an H2O cluster, and if you aren’t already running MinIO, please download and install it. In addition, please download and install the aws.s3 R library.
Statistical arbitrage
The notion of statistical arbitrage is that there exists a somewhat dependable relationship between the movements of the prices of 2 instruments or assets. In this case, we will be using currency pairs as the instruments. If the relationship between the pairs is fairly stable, then any deviation from that relationship would likely be followed by a reversion back to the stable relationship. This implies that when there is a deviation, we have the opportunity to take a position and potentially profit, assuming the relationship reverts.
A classic example of two assets that are assumed to have a stable relationship is the equity prices of similar-sized companies in a given industry. Let’s take technology - Looking at the movement of two companies of similar size in the technology industry, the assumption is that they will each be equally impacted by changes to the industry as a whole such as the cost of similarly trained labor, interest rates, supply shortages, etc. We should be able to discern a relationship between the equity prices of these companies, and should we see a deviation, it might be an opportunity to profit if we believe that the relative equity prices will revert back to the previously observed relationship. Of course, deviations from the underlying relationship could be caused by intentional changes in the business models of one or both of the companies, so a deviation is not a guarantee of a profit opportunity.
Another common example is automobile companies, as explained in this Investopedia article explaining Statistical Arbitrage or this Wikipedia article on Statistical Arbitrage.
Evaluating the underlying relationship between the time series of the prices for the instruments is an area of deep study in statistics or econometrics. This is a simplified tutorial and provides 2 simple approaches. The first simply takes the difference between the instruments and uses a rolling 10-day mean and standard deviation for determining the points of deviation from the relationship. The second uses some history to build an ML model using H2O AutoML, then applies that model to predict the relationship that should exist between the instruments going forward. The actual difference between the instruments on a given day is compared to the predicted value and the difference between actual and predicted is used to determine the points of deviation from the relationship.
The tutorial
For this tutorial, I’m starting with two currency pairs - eurjpy and gbpusd
Currency pairs are specified using two currencies each - eurjpy is the exchange rate for 1 Euro in terms of Yen. The Euro is the “base currency,” and the Yen is the “quote currency.” The exchange rate - of the price of this instrument - is the number of Yen it takes to buy one Euro. At the moment, Google says it takes 146.57 Yen to buy one Euro.
Similarly, the gbpusd currency pair has a base currency of British Pounds and a quote currency of US Dollars. The exchange rate, or the price of this instrument, is the number of USD it takes to buy 1 Euro. Again, according to Google, the rate is 1.13 - At the moment, it takes 1.13 USD to buy one Euro.
Exchange rates, like all instruments traded in a market, have some number of sellers and some number of buyers, and the sellers “Ask” for a price in hopes someone will pay it, and the bidders “Bid” an amount. When those figures are the same between a seller and a buyer, a “Trade” occurs. When building something like statistical arbitrage for real, it is important to understand the structure of how markets work and the typical “Spread” between the bid and ask since the trading algorithm will be subject to that spread. Needless to say, this tutorial is for informational purposes only and should not be used for trading as it stands.
We will explore two approaches to determining the underlying relationship between these currencies. Experiment 1 uses the recent historical relationship between them to predict what the relationship should be. Any deviation from what recent history predicts would be a potential opportunity to trade. I’ve chosen (pretty randomly) using a 10-day history to calculate the mean and standard deviation of the differences between the currency pairs. Experiment 2 uses H2O AutoML to build a model to predict the relationship based on training data from the first half of the year. These are certainly not the only ways to gain an understanding of the relationship. Most professional approaches are significantly more complex and require a fairly deep capability in statistics or econometrics. Such approaches are beyond what we can cover in this tutorial.
The data
The data comes from TraderMade, as previously mentioned, and I’m using the daily time series. This data provides the market open, high, low, and close for each day. The notion of “market” is a bit of a misnomer in forex since there is not a single clearinghouse-based market for the exchange of currencies, but rather a number of markets, and prices may vary across these markets. Additionally, forex is a continuous market, so the notion of a market open and close are manufactured. Since I would like to have a single data point that represents each day, I am choosing to average the open, high, and low for each day and use that average as a single exchange rate for a given day. The takeaway of this is that the “daily price” data point that I am using to represent a “day” is really, really, averaged for this tutorial. This will kill some of the potential performance of the experiments but makes the explanation easier.
Rather than storing this data as CSV files or storing it in a database such as MySQL, MariaDB, PostgreSQL, or another, I find it much easier to leverage the newer “Open Table Standards” file formats and to store the data in an object store. MinIO is an excellent choice for this use case.
For this tutorial, I’m storing the files in Parquet format, but there are several new formats that provide the convenience of working with files combined with the power of table structures. In this case, I bring down the raw data from TraderMade and partition it by date. Partitioning by date is similar to creating an index on the date in DB terms.
The resulting saved data looks like this. Within the prefix of “eurjpy”, for instance, the data is written as multiple files partitioned by the specified field.
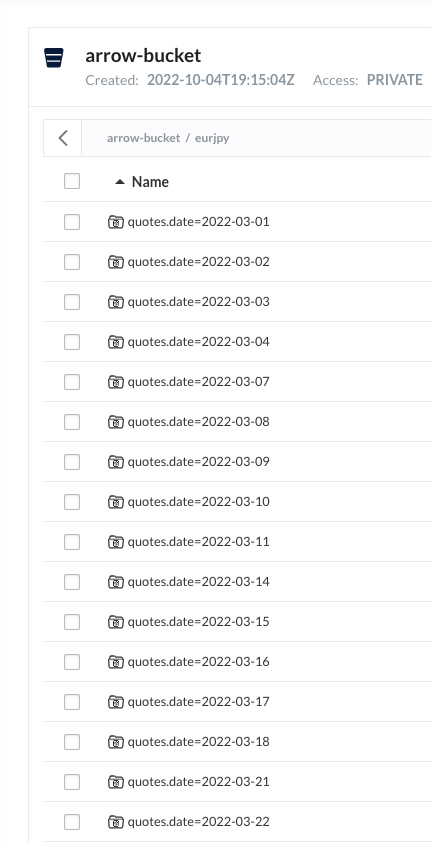
This means that selected retrieval (retrieving a date range for instance) only reads the related files. This approach is very efficient compared to storing data in a CSV where it is typical to load the whole file and then select in memory. It is also much more convenient than standing up a separate database with all the required configuration, drivers, and maintenance.
Here is the R code to store this data:
# get the data from TraderMade and store as Parquet partitioned by date
ccy1_dataframe_tick<-GetCCYTimeseries(ccy1,start_date,end_date)
ccy1_dataframe_tick %>%
group_by(quotes.date) %>%
write_dataset(GetMinIOURI(ccy1), format = "parquet" )The first line retrieves the data from TraderMade using a function to hide the creation of the URL, etc. The second is a pipeline that pipes the dataframe through the Dplyr “group_by” predicate and then pipes it to a function that writes the data to my MinIO cluster as Parquet. The “group_by” directive causes the data to be partitioned by “quotes.date”, as shown earlier. It could not be easier.
Retrieval of data is just as easy. Here is the R code to retrieve all the data for this ccy into a dataframe:
df1 <- open_dataset(GetMinIOURI(ccy1), format = "parquet") %>% collect()The above code resulted in a dataframe with 132 rows - all the data that I had stored. Selecting a subset of the rows is just as easy. Here I only load data after “2022-04-01”:
df1 <- open_dataset(GetMinIOURI(ccy1), format = "parquet") %>% filter(quotes.date > "2022-04-01") %>% collect()Notice the use of a filter to specify the “where clause” for loading the data. This is dirt simple and does not require the care and feeding of an external database. Performance is exceptional on MinIO object storage as well since only the requested data is loaded, assuming the partitioning is correct.
Back to the problem at hand
In order to create a single time series representing the relationship between these two instruments, I start by taking the difference between the rates for them - meaning I subtract the daily price of one from the other. In order to see where that value is relative to the “existing relationship” between the two instruments, I compare it in turn of standard deviations using the mean of the preceding 10-days differences.
What? Yes, calculate the difference between the rates for each day. For each day, calculate the mean of the differences for the preceding 10 days. Then determine how far from this mean value today’s rate is in terms of standard deviations.
Here is an example. Below is the chart for 3/1/2022 - 8/31/2022. This chart takes eurjpy and subtracts gbpusd to get the difference. It then plots each point as the standard deviation from the preceding 10-day mean of that difference. So at its peak, this is roughly 2.3 standard deviations above the mean of the preceding 10 days difference. And at its lowest, this is roughly 2.7 standard deviations below the mean of the preceding 10 days difference. The red hash lines are at 1.5 standard deviations above and below for visual reference.
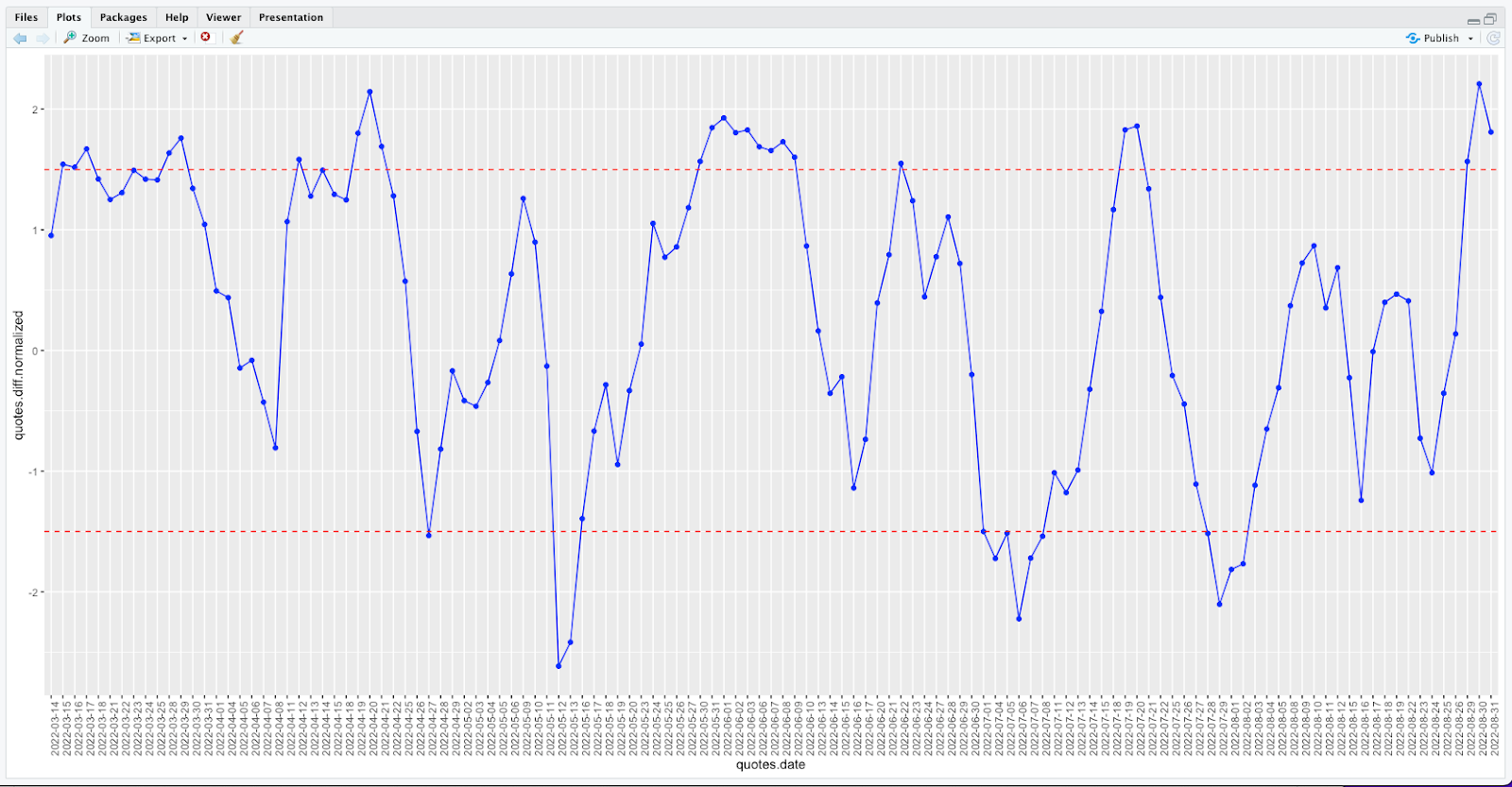
What is nice about this data representation is that it varies fairly equally above and below zero. We are proposing that the zero line (the mean of the preceding 10 days difference) represents the underlying relationship and when the data moves away from the line, we believe it will revert back subsequently.
We see the normalized difference between the two currencies breaking the upper and lower threshold a number of times. Remember, the thresholds I have chosen are arbitrary, and it is not required that they be symmetric around the mean. Also, the units on the Y axis are in standard deviations. Since the data is unlikely to be normally distributed or gaussian distributed, the notion of a standard deviation doesn’t really hold. Yet, it provides an easy way to talk about the distance from the mean of any individual measurement, so we will use it.
Interpretation
Nice line; what does it mean? When the blue line is high, it implies that the difference (eurjpy minus gbpusd) is large relative to the preceding 10 days - meaning that eurjpy is expensive in terms of gbpusd. When this happens, we believe the eurjpy will drop, and gbpusd will rise (so the line will move toward “zero” - the mean of the preceding 10 days difference). When the blue line is low, it implies that the difference is small, and we believe eurjpy will move up relative to gbpusd in the near future in order to move toward “zero.”
When the blue line is high, we want to sell eurjpy (sell eur and take our proceeds in terms of jpy) to take advantage of the expected reversion. At the same time, we want to buy gbpusd (buy gbp and pay for it in terms of usd). We would do this because we believe the eurjpy exchange rate is high relative to the gbpusd exchange rate based on the history we are considering. When the blue line is low, we want to buy eurjpy and sell gpbusd for similar reasons - we believe that the movements of the exchange rates will soon change, and we believe we can profit.
What does it mean to sell eur? Well, I’m in the United States, and I generally hold US Dollars (usd), so in order to sell eur, I have to have first bought some Euros using my US Dollars. To run this tutorial, I need some of each of these currencies to start trading since I might need to give up any of them as part of the trades, and I can’t give away what I don’t own.
So how do we do this? First, we start with some notion of a “starting balance” in a given currency - for me, it will be US dollars. We then buy some of each of the currencies we will possibly trade. So I buy eurusd, jpyusd, gbpusd, usdusd - I buy the ccys I might need and pay for those ccys using my usd. Notice the last one isn’t really buying anything. At the end of each experiment, I will liquidate these ccys back into usd to evaluate the performance.
Once we have some of the ccys we will need, we then trade based on the signals. When we are finished and have liquidated our ccys to US Dollars, we can see if we made or lost money. Simple but effective.
Using MinIO and Parquet for AI/ML and data analytics on financial data
I’m using MinIO, which is a 100% S3-compatible object store. The data is downloaded and stored as Parquet files. Parquet is one of the newer tabular file formats that are a highly efficient replacement for CSV files. Parquet, and other “open standards” files, are quickly replacing CSV data storage and replacing proprietary database storage formats - most database products are now able to use external Parquet files as “external tables.” This means there is a separation between the functionality the database product provides (indexing and querying, etc.), from the underlying storage format. This is a wonderful advancement for data users. Parquet files (or ORC, or Hudi, or Iceberg - there are lots of open standards now) residing on MinIO S3 storage provide a highly efficient and cost-effective data storage solution for AI/ML and analytics workloads.
I’m also using R and H2O. If you have read my previous blogs, these are two of my favorite products for this type of work.
Experiment one
To start with, I created an R script file to load the required packages called packages.R:
#load necessary libraries
if (!require("httr")) {
install.packages("httr")
library (httr)
}
if (!require("jsonlite")) {
install.packages("jsonlite")
library (jsonlite)
}
if (!require("ggplot2")) {
install.packages("ggplot2")
library(ggplot2)
}
if (!require("arrow")) {
install.packages("arrow")
library(arrow)
}
if (!require("dplyr")) {
install.packages("dplyr")
library(dplyr)
}
if (!require("zoo")) {
install.packages("zoo")
library(zoo)
}
if (!require("aws.s3")) {
install.packages("aws.s3")
library(aws.s3)
}
if (!require("lubridate")) {
install.packages("lubridate")
library(lubridate)
}
if (!require("quantmod")) {
install.packages("quantmod")
library(quantmod)
}
if (!require("zoo")) {
install.packages("zoo")
library(zoo)
}
if (!require("h2o")) {
install.packages("h2o")
library(h2o)
}
GetMinIOURI <- function(prefix) {
# get minio config, with expected defaults
minio_key <- Sys.getenv("MINIO_ACCESS_KEY", "minioadmin")
minio_secret <- Sys.getenv("MINIO_SECRET_KEY", "minioadmin")
minio_host <- Sys.getenv("MINIO_HOST", "Your MinIO Host IP address")
minio_port <- Sys.getenv("MINIO_PORT", "Your MinIO Port")
minio_arrow_bucket <- Sys.getenv("MINIO_ARROW_BUCKET", "arrow-bucket")
# helper function for minio URIs
minio_path <- function(...) paste(minio_arrow_bucket, ..., sep = "/")
minio_uri <- function(...) {
template <- "s3://%s:%s@%s?scheme=http&endpoint_override=%s%s%s"
sprintf(template, minio_key, minio_secret, minio_path(...), minio_host, ":", minio_port)
}
return(minio_uri(prefix))
}Next, I created some data retrieval functions to get data from Tradermade in an R script, DataFunctions.R:
source("packages.R")
# using TraderMade
# https://marketdata.tradermade.com
# uses an api_key
api_key <- "Your Free TraderMade API Key"
GetCCYList <- function(...) {
# get list of ccys
req <- paste0("https://marketdata.tradermade.com/api/v1/historical_currencies_list?api_key=",api_key)
data_raw <- GET(url = req)
data_text <- content(data_raw, "text", encoding = "UTF-8")
data_json <- fromJSON(data_text, flatten=TRUE)
dataframe <- as.data.frame(data_json)
# this is like 9700 rows
return(dataframe)
}
GetCCYRates <- function(ccy1,ccy2) {
#get current rates
req <- paste0("https://marketdata.tradermade.com/api/v1/live?currency=",toupper(ccy1),",",ccy2,"&api_key=",api_key)
data_raw <- GET(url = req)
data_text <- content(data_raw, "text", encoding = "UTF-8")
data_json <- fromJSON(data_text, flatten=TRUE)
dataframe <- as.data.frame(data_json)
return(dataframe)
}
GetCCYTimeseries <- function(ccy,start_date,end_date) {
# get timeseries historical data for ccy
tick_req <- paste0("https://marketdata.tradermade.com/api/v1/timeseries?currency=",
toupper(ccy),"&api_key=",api_key,"&start_date=",
start_date,"&end_date=",end_date,"&format=records",collapse="")
data_tick_raw <- GET(url = tick_req)
data_tick_text <- content(data_tick_raw, "text", encoding = "UTF-8")
data_tick_json <- fromJSON(data_tick_text, flatten=TRUE)
dataframe_tick <- as.data.frame(data_tick_json)
dataframe_tick$quotes.avg <-
(dataframe_tick$quotes.open + dataframe_tick$quotes.high + dataframe_tick$quotes.low)/3
dataframe_tick$quotes.date <- ymd(dataframe_tick$quotes.date)
#sort by date
dataframe_tick <- dataframe_tick[order(dataframe_tick$quotes.date),]
return(dataframe_tick)
}These data functions are used by the following DataFrame functions, DFFunctions.R since dataframes is how R processes data:
source("packages.R")
source("DataFunctions.R")
DownloadCCYDF <- function(ccy1, start_date, end_date) {
# get the data
ccy1_dataframe_tick<-GetCCYTimeseries(ccy1,start_date,end_date)
ccy1_dataframe_tick %>%
group_by(quotes.date) %>%
write_dataset(GetMinIOURI(ccy1), format = "parquet" )
return (ccy1_dataframe_tick)
}
DownloadCCYDFs <- function(ccy1, ccy2, start_date, end_date) {
# get the data
ccy1_dataframe_tick<-GetCCYTimeseries(ccy1,start_date,end_date)
ccy1_dataframe_tick %>%
group_by(quotes.date) %>%
write_dataset(GetMinIOURI(ccy1), format = "parquet" )
ccy2_dataframe_tick<-GetCCYTimeseries(ccy2,start_date,end_date)
ccy2_dataframe_tick %>%
group_by(quotes.date) %>%
write_dataset(GetMinIOURI(ccy2), format = "parquet" )
return (list(ccy1_dataframe_tick, ccy2_dataframe_tick))
}
LoadCCYDF <-function(ccy1) {
df1 <- open_dataset(GetMinIOURI(ccy1), format = "parquet") %>% collect()
return(df1)
}
LoadCCYDFs <-function(ccy1, ccy2) {
df1 <- open_dataset(GetMinIOURI(ccy1), format = "parquet") %>% collect()
df2 <- open_dataset(GetMinIOURI(ccy2), format = "parquet") %>% collect()
return(list(df1,df2))
}
CreateJointDF<-function(ccy1_df,ccy2_df,rolling_period) {
# we believe this relationship should be stable
joint_df <- inner_join(ccy1_df,ccy2_df, by = 'quotes.date')
# order by date
joint_df<- joint_df[order(joint_df$quotes.date),]
# ok, simple case, the relationship between ccy1 and ccy2 is absolute, so just subtract
joint_df$quotes.diff <- joint_df$quotes.avg.x - joint_df$quotes.avg.y
# add a rolling mean and sd at 10 days
joint_df <- joint_df %>%
mutate(rolling.mean = rollmean(quotes.diff, k=rolling_period, fill=NA, align='right')) %>%
mutate(rolling.sd = rollapplyr(quotes.diff, rolling_period, sd, fill = NA))
# remove the NAs in the beginning of the rolling mean
joint_df <- joint_df[complete.cases(joint_df), ]
joint_df$quotes.diff.normalized <-
(joint_df$quotes.diff - joint_df$rolling.mean) / joint_df$rolling.sd
# # write this as parquet files
# joint_df %>%
# write_dataset(GetMinIOURI(paste0(ccy1,"-",ccy2)), format = "parquet" )
return (joint_df)
}
CreateLaggedDF<-function(ccy1_df,ccy2_df,lag) {
# we believe this relationship should be stable
tmp_df <- inner_join(ccy1_df,ccy2_df, by = 'quotes.date')
# sort the result
tmp_df<-tmp_df[order(tmp_df$quotes.date),]
# we are going to predict this difference
tmp_df$quotes.diff <- tmp_df$quotes.avg.x - tmp_df$quotes.avg.y
#save off date vector
df.date<-tmp_df$quotes.date
#save off the target
df.target<-tmp_df$quotes.diff
#save off the data that we are going to lag
df.data<-tmp_df$quotes.diff
df.data<-zoo(df.data,df.date)
#create lagged df
df.data.lag<-Lag(df.data,k=1:lag)
df.data.lag<-as.data.frame(df.data.lag)
# cbind the date and target on the front
lagged_df<-cbind(df.date,df.target,df.data.lag)
lagged_df<-lagged_df[complete.cases(lagged_df),]
lagged_df$df.date <- ymd(lagged_df$df.date)
# # write this as parquet files
# lagged_df %>%
# write_dataset(GetMinIOURI(paste0(ccy1,"-",ccy2,"-lagged-",lag)), format = "parquet" )
# this is a file that can be used for training a model
return (lagged_df)
}In order to evaluate the results of these experiments, we will need some back-testing functions. Here is that file, TestFunctions.R:
source("packages.R")
source("DFFunctions.R")
TestActionsDF<-function(ccy1,ccy2,actions_df,startingUSD,start_date,end_date) {
# start with an equal amount (in USD) of each)
USDBal <- startingUSD
x = floor(USDBal/4)
#load the data - get each in terms of USD
c1<-toupper(paste0(substring(ccy1,1,3),"USD"))
c2<-toupper(paste0(substring(ccy1,4,6),"USD"))
c3<-toupper(paste0(substring(ccy2,1,3),"USD"))
c4<-toupper(paste0(substring(ccy2,4,6),"USD"))
# get the individual currency / USD rates
if (c1 != "USDUSD") {
#c1_df<- DownloadCCYDF(c1,start_date,end_date)
c1_df <- LoadCCYDF(c1)
p_c1 <- (c1_df %>% filter(quotes.date == ymd(start_date)))$quotes.avg
c1_bal <- floor(x/p_c1)
USDBal <- USDBal - (c1_bal*p_c1)
c1_trade_amt <- floor(c1_bal/20)
} else {
c1_bal = x
USDBal = USDBal - x
}
if (c2 != "USDUSD") {
#c2_df<- DownloadCCYDF(c2,start_date,end_date)
c2_df <- LoadCCYDF(c2)
p_c2 <- (c2_df %>% filter(quotes.date == ymd(start_date)))$quotes.avg
c2_bal <- floor(x/p_c2)
USDBal <- USDBal - (c2_bal*p_c2)
c2_trade_amt <- floor(c2_bal/20)
} else {
c2_bal = x
USDBal = USDBal - x
}
if (c3 != "USDUSD") {
#c3_df<- DownloadCCYDF(c3,start_date,end_date)
c3_df <- LoadCCYDF(c3)
p_c3 <- (c3_df %>% filter(quotes.date == ymd(start_date)))$quotes.avg
c3_bal <- floor(x/p_c3)
USDBal <- USDBal - (c3_bal*p_c3)
c3_trade_amt <- floor(c3_bal/20)
} else {
c3_bal = x
USDBal = USDBal - x
}
if (c4 != "USDUSD") {
#c4_df<- DownloadCCYDF(c4,start_date,end_date)
c4_df <- LoadCCYDF(c4)
p_c4 <- (c4_df %>% filter(quotes.date == ymd(start_date)))$quotes.avg
c4_bal <- floor(x/p_c4)
USDBal <- USDBal - (c4_bal*p_c4)
c4_trade_amt <- floor(c4_bal/20)
} else {
c4_bal = x
USDBal = USDBal - x
}
# OK, we have a balance in each of the desired currencies, and we have a notion of the trade amount
# apply the trades and see what happens
actions <- actions_df %>% filter (quotes.date > ymd(start_date) & quotes.date <= ymd(end_date))
# apply the trades
for (row in 1:nrow(actions)) {
# figure out what we are buying and selling and get the rates on the specified dates
d = actions[row,1]
buy.ccy = actions[row,2]
sell.ccy = actions[row,3]
# handle the buy
if (buy.ccy == ccy1) {
# get he exchange rate on this date
ex_rate = (ccy1_df %>% filter(quotes.date == ymd(d)))$quotes.avg
if (c2_bal >= c1_trade_amt / ex_rate) {
c1_bal = c1_bal + c1_trade_amt
c2_bal = c2_bal - (c1_trade_amt * ex_rate)
}
} else {
# get he exchange rate on this date
ex_rate = (ccy2_df %>% filter(quotes.date == ymd(d)))$quotes.avg
if (c4_bal >= c3_trade_amt / ex_rate) {
c3_bal = c3_bal + c3_trade_amt
c4_bal = c4_bal - (c3_trade_amt * ex_rate)
}
}
#handle the sell
if (sell.ccy == ccy1) {
# get he exchange rate on this date
ex_rate = (ccy1_df %>% filter(quotes.date == ymd(d)))$quotes.avg
if (c1_bal >= c1_trade_amt) {
c1_bal = c1_bal - c1_trade_amt
c2_bal = c2_bal + (c1_trade_amt * ex_rate)
}
} else {
# get he exchange rate on this date
ex_rate = (ccy2_df %>% filter(quotes.date == ymd(d)))$quotes.avg
if (c3_bal >= c3_trade_amt) {
c3_bal = c3_bal - c3_trade_amt
c4_bal = c4_bal + (c3_trade_amt * ex_rate)
}
}
}
# unwind and accumulate the balance in USD
# get the end quotes for individual currency / USD at the end date
if (c1 != "USDUSD") {
p_c1 <-c1_df[c1_df$quotes.date==end_date,]$quotes.avg
USDBal <- USDBal + (c1_bal * p_c1)
} else {
USDBal <- USDBal + c1_bal
}
if (c2 != "USDUSD") {
p_c2 <- c2_df[c2_df$quotes.date==end_date,]$quotes.avg
USDBal <- USDBal + (c2_bal * p_c2)
} else {
USDBal <- USDBal + c1_bal
}
if (c3 != "USDUSD") {
p_c3 <- c3_df[c3_df$quotes.date==end_date,]$quotes.avg
USDBal <- USDBal + (c3_bal * p_c3)
} else {
USDBal <- USDBal + c1_bal
}
if (c4 != "USDUSD") {
p_c4 <- c4_df[c4_df$quotes.date==end_date,]$quotes.avg
USDBal <- USDBal + (c4_bal * p_c4)
} else {
USDBal <- USDBal + c1_bal
}
return ((USDBal-startingUSD)/startingUSD)
}For the first experiment, here is the main file, MainAbsolute.R, reads the data, wrangles it, determines some buy and sell points, and finally back-tests the result.
source("packages.R")
source ("DFFunctions.R")
source ("TestFunctions.R")
ccy1 = "eurjpy"
ccy2 = "gbpusd"
# these are used to get the data
start_date="2022-06-01"
end_date="2022-08-31"
# Adding buy/sell indicator
sd_threshold <- 1.5
# load the data
#df_list <- DownloadCCYDFs(ccy1,ccy2, start_date, end_date)
df_list <- LoadCCYDFs(ccy1,ccy2)
ccy1_df<-df_list[[1]]
ccy2_df<-df_list[[2]]
#sort these
ccy1_df<-ccy1_df[order(ccy1_df$quotes.date),]
ccy2_df<-ccy2_df[order(ccy2_df$quotes.date),]
# Test 1 - straight stat-arb using subtraction
joint_df<-CreateJointDF(ccy1_df,ccy2_df,10)
# graph these
ggplot(aes(x = quotes.date, y = quotes.diff.normalized, group=1), data = joint_df) +
geom_point(color = "blue") +
geom_line(color = "blue") +
geom_hline(yintercept=sd_threshold, linetype="dashed",
color = "red") +
geom_hline(yintercept=-sd_threshold, linetype="dashed",
color = "red") +
theme(axis.text.x = element_text(angle = 90))
joint_df <- joint_df %>%
mutate(sell = case_when(
quotes.diff.normalized > sd_threshold ~ ccy1,
quotes.diff.normalized < (-1*sd_threshold) ~ ccy2)) %>%
mutate(buy = case_when(
quotes.diff.normalized > sd_threshold ~ ccy2,
quotes.diff.normalized < (-1*sd_threshold) ~ ccy1))
# get rid of some unnecessary cols
joint_df <- joint_df %>% select(quotes.date,quotes.diff.normalized,buy,sell)
actions_df <- joint_df[,c('quotes.date','buy','sell')]
actions_df <- actions_df[complete.cases(actions_df), ]
startingUSD=10000
ret <- TestActionsDF(ccy1,ccy2,actions_df,startingUSD,start_date,end_date)
retLet’s discuss the results of Experiment One. There are a few things to point out:
- The period of time we are testing this for is 6/1/2022 - 8/31/2022
- Simply moving some USD into these currencies at the start of the period and then back into USD at the end has a performance of -0.0675 or -6.75% We will use this as our “null hypothesis.” If we don’t place any trades, then this is the return - this is what we have to beat with our indicator system.
- If we use subtraction to define the relationship and use a 10-day rolling mean as the baseline, the performance is -0.06616 or roughly -6.62%. This is better than not trading at all, so we are moving in the right direction.
- And, of course, we are ignoring a whole bunch of real-world considerations, like any fees associated with these trades that would impact returns.
Experiment Two
Can we do better by using machine learning to define/predict the relationship between these instruments and create more profitable trades? I’m using the AutoML capabilities of H2O to build a model that predicts what the difference between the currencies should be (given the data it was trained on). I’m then comparing the actual difference, and if the actual and the predicted values don’t agree, then it appears to be a trading opportunity.
We need a couple more files to test that, the first being MLFunctions.R:
source("Packages.R")
# initialize the h2o server
h2o.init(ip="Your H2O host IP address", port=54321, startH2O=FALSE,
jvm_custom_args = "-Dsys.ai.h2o.persist.s3.endPoint=”http://Your MinIO Host”:9000 -Dsys.ai.h2o.persist.s3.enable.path.style=true")
h2o.set_s3_credentials("Your MinIO Access Key", "Your MinIO Secret Key")
TrainModel<-function(training_df) {
training_df.hex<-as.h2o(training_df, destination_frame= "training_df.hex")
splits <- h2o.splitFrame(data = training_df.hex,
ratios = c(0.6), #partition data into 60%, 40%
seed = 1) #setting a seed will guarantee reproducibility
train_hex <- splits[[1]]
test_hex <- splits[[2]]
y_value <- 1
predictors <- c(2:ncol(train_hex))
# train
aml = h2o.automl(y=y_value,x=predictors,
training_frame=train_hex,
leaderboard_frame = test_hex,
max_runtime_secs = 60,
seed = 1)
model<-aml@leader
# train model
# model <- h2o.deeplearning(y=y_value, x=predictors,
# training_frame=train_hex,
# activation="Tanh",
# autoencoder=FALSE,
# hidden=c(50),
# l1=1e-5,
# ignore_const_cols=FALSE,
# epochs=1)
# save the leader model as bin
model_path <- h2o.saveModel(model, path = "s3://bin-models/stat_arb_model_bin")
return(model)
}
RunModel<-function(model,pred_df) {
pred_df.hex<-as.h2o(pred_df)
pred.hex <- h2o.predict(model, pred_df.hex) # predict(aml, test) and h2o.predict(aml@leader, test) also work
pred<-as.data.frame(pred.hex)
return(pred)
}And a new MainModel.R to exercise the model approach
source("Packages.R")
source ("DFFunctions.R")
source("MLFunctions.R")
source ("TestFunctions.R")
# Example of multiple approaches to stat arb in forex
ccy1 = "eurjpy"
ccy2 = "gbpusd"
# these are used to get the data
start_date="2022-03-01"
end_date="2022-08-31"
start_training_date = "2022-03-01"
end_training_date = "2022-05-31"
start_pred_date = "2022-06-01"
end_pred_date = "2022-08-31"
# load the data
#df_list <- DownloadCCYDFs(ccy1,ccy2, start_date, end_date)
df_list <- LoadCCYDFs(ccy1,ccy2)
ccy1_df<-df_list[[1]][,c("quotes.date","quotes.avg")]
ccy2_df<-df_list[[2]][,c("quotes.date","quotes.avg")]
#sort these
ccy1_df<-ccy1_df[order(ccy1_df$quotes.date),]
ccy2_df<-ccy2_df[order(ccy2_df$quotes.date),]
# Test 2 - arb using a model to predict the difference
lagged_df<-CreateLaggedDF(ccy1_df,ccy2_df,10)
# create the training df
training_df <- lagged_df %>% filter(df.date > ymd(start_training_date), df.date <= ymd(end_training_date))
#get rid of the date training_df
training_df<-training_df[-1]
# create the pred df
pred_df <- lagged_df %>% filter(df.date > ymd(start_pred_date), df.date <= ymd(end_pred_date))
#write the files out
training_df %>% write_dataset(GetMinIOURI("training_df"), format = "parquet" )
pred_df %>% write_dataset(GetMinIOURI("pred_df"), format = "parquet" )
#train the model on this data
model <- TrainModel(training_df)
model
# okay, run the model on the data from 6/1 to 8/31
# it's ok that date and target are in here, the model selects the X values by col name
pred<-RunModel(model,pred_df)
# wrangle the return
predictions<-cbind(quotes.date=pred_df$df.date,actual=pred_df$df.target,pred=pred)
predictions$quotes.date<-as.Date(predictions$quotes.date)
predictions$diff<-predictions$actual-predictions$pred
# Adding buy/sell indicator
upper_threshold <- 5.0
lower_threshold <- 0.5
ggplot(aes(x = quotes.date, y = diff, group=1), data = predictions) +
geom_point(color = "blue") +
geom_line(color = "blue") +
geom_hline(yintercept=upper_threshold, linetype="dashed",
color = "red") +
geom_hline(yintercept=lower_threshold, linetype="dashed",
color = "red") +
theme(axis.text.x = element_text(angle = 90))
predictions <- predictions %>%
mutate(sell = case_when(
diff > upper_threshold ~ ccy1,
diff < (lower_threshold) ~ ccy2)) %>%
mutate(buy = case_when(
diff > upper_threshold ~ ccy2,
diff < (lower_threshold) ~ ccy1))
actions_df <- predictions %>% select(quotes.date,buy,sell) %>% filter(! is.na(buy))
# Let's test it for 6/1 - 8/31
startingUSD=10000
ret <- TestActionsDF(ccy1,ccy2,actions_df,startingUSD,start_date,end_date)
retNotice in the modeling functions, we run H2O AutoML and allow it to select the best model from those it tries. The parameters we use for the AutoML execution are simply intended for this demo. Once the model is selected, we save it back to MinIO in a binary format that allows it to be executed from a production workflow without R. The model could be stored in a model repository, but honestly I’ve found that often those are a bit overkill. Storing the model directly along with some metadata about the model is often sufficient.
Using the modeling approach to identify the differences is a little more involved. I used the data from 3/1/2022 to 5/31/2022 to create a “Lagged” training set of 10 days. This is valid but is the most basic approach to training a model on time series data and has a number of issues and drawbacks. I am using the Lagged training data with H2O AutoML to train a model to be able to predict the difference. We use this prediction as the expected difference between the ccys instead of the rolling mean, as we did in the first experiment. If you are interested in processing time series data for use with AI/ML, here is a good Time Series Forecasting Blog from H2O. Additionally, there is a recommendation at the end of this article for a book by author Marcos Lopez De Prado that is a much deeper treatment of this complex topic.
Here is a graph of the differences between what the model predicted and the actuals for the period of 6/1/2022 to 8/31/2022
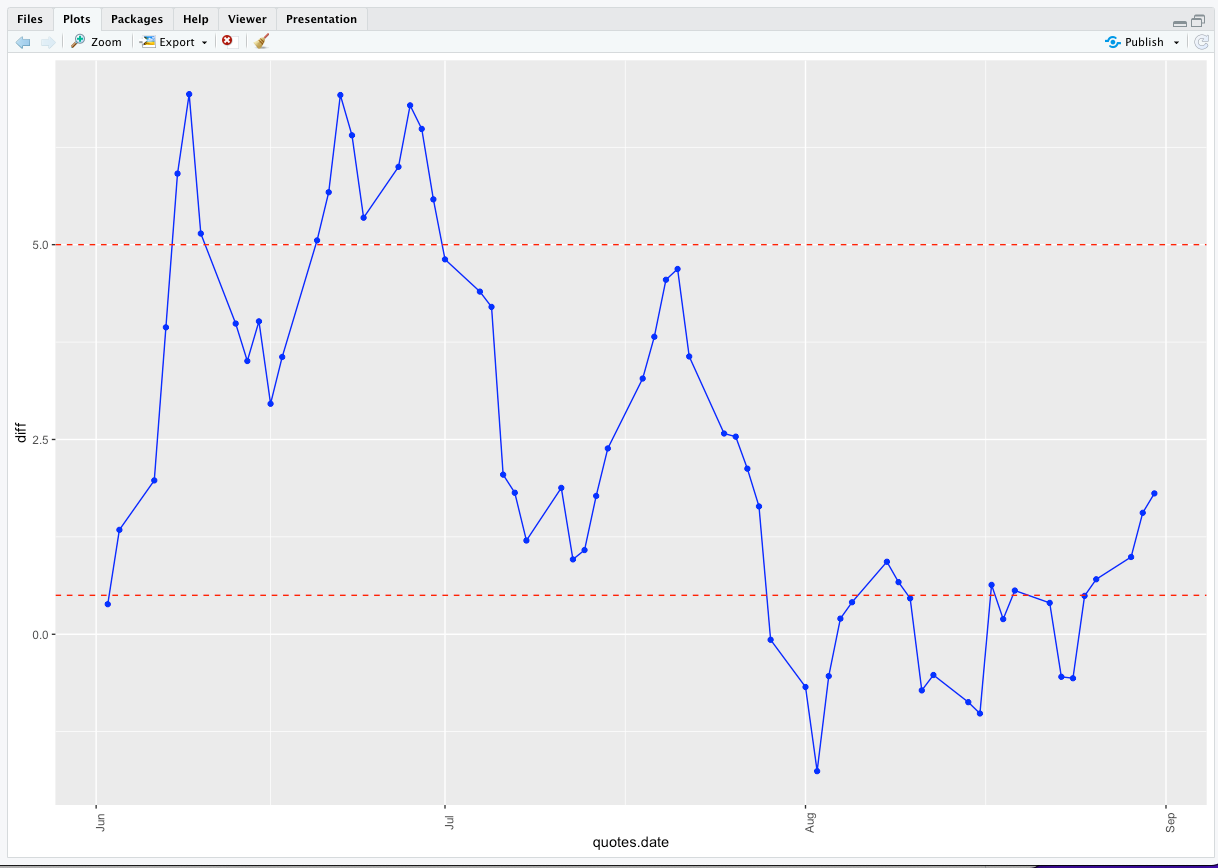
Let’s take a look at the results of Experiment Two.
How did we do? The null hypothesis for this set of experiments is -6.75% The first Experiment - using the rolling mean static relationship and trading as indicated, had a performance of -6.62%. This is a little better and at least moving in the right direction.
Using an AutoML model trained on the lagged historical relationship and then using that approach to predict the difference allowed us to improve the return slightly. With this approach, the performance is -0.05997 or roughly -6.0%, slightly better than the previous experiment.
Could we do better - sure? These two experiments are severely limited and are for instructional purposes only. Every forex trader has their own methodology, so I’ve tried to provide a process that can easily be customized. There are many financial avenues to pursue to improve on the approaches outlined here.
Regardless of our financial strategy, our technical avenue is clear – cloud-native MinIO object storage has the performance and resiliency to power a wide variety of statistical and AI/ML workloads. Software-defined, S3-compatible, and blisteringly performant MinIO is the standard for such workloads. This is why MinIO comes standard with Kubeflow and works seamlessly with every major AI/ML framework, including H2O and TensorFlow.
Conclusion
This tutorial looked at using statistical arbitrage between a pair of the exchange rate - eurjpy and gbpusd. There are many others to explore. It looked at only “daily bars” (open, high, low, close data). There are other timeframes or granularities to be explored - “hour bars,” “minute bars,” “second bars,” as well as actual tick data - which are not homogenous in the time domain and require some additional processing.
If you are interested in financial algorithms and processing financial data, I recommend An Introduction to High-Frequency Finance. The authors discuss the value and use of high-frequency (tick-by-tick) data for understanding market microstructure, including a discussion of the best mathematical models and tools for dealing with such vast amounts of data. The examples, and many of the topics, related to forex.
If you are interested in applying machine learning to financial data, I recommend Advances in Financial Machine Learning. The author provides practical insight into using advanced ML solutions to overcome real-world investment problems.
There is a sea change taking place in the database and analytics market that opens financial (and other) data for greater collaboration and insight. In recent years, many databases and analytics packages have embraced open table standards, such as Parquet, Arrow, Iceberg, and Hudi. There is little doubt that the days of databases and analytics products being limited to proprietary file formats are coming to a close. These open tabular data standards allow for greater processing flexibility with no loss of storage efficiency. They also allow for the movement of the data between products - Big Query data that is stored in an open file format can be accessed from Snowflake as an external table, for example. Open file formats are optimized for object storage. Parquet files created in this tutorial for instance can be accessed from data management and analytics programs capable of incorporating external tables using open table formats. They are a natural fit for MinIO object storage because of its cloud-native and ubiquitous nature. Similarly, for on-prem deployments, object storage running on commodity hardware increases value for customers. Competition between hardware vendors for commodity hardware guarantees low cost and high value.
The future is open, cloud-native, and distributed.






